각의 등분선

원문 보기: https://dawoum.duckdns.org/wiki/각의_등분선

See also: Angle bisector theorem

중선 정리와 함께 간혹 혼동되는 것이 각의 이등분선입니다. 여기서는 일반적인 각의 등분선의 특징에 대해 논의를 하고, 자주 이용되는 각의 이등분선에 대해 결과를 알아보겠습니다.

내각의 등분선

\(\triangle \mathrm{ABC}\)에서 \(\angle \mathrm A\)를 \(\angle \alpha\)와 \(\angle \beta\)로 나누어진다고 할 때, \(\triangle \mathrm{ABN}\)의 넓이 \(\mathrm S_1\)과 \(\triangle \mathrm{ACN}\)의 넓이 \(\mathrm S_2\)는 다음과 같이 구해집니다.

\(\quad\)\(\displaystyle \mathrm S_1=\frac{1}{2}\mathrm{AB\cdot AN}\sin\alpha\)

\(\quad\)\(\displaystyle \mathrm S_2=\frac{1}{2}\mathrm{AC\cdot AN}\sin\beta\)

한편, \(\triangle \mathrm{ABN}\)과 \(\triangle \mathrm{ACN}\)의 꼭짓점 \(\mathrm A\)에서 변 \(\mathrm{BC}\)에 내린 수선의 발을 \(\mathrm H\)라 하면, 높이 \(\mathrm{AH}\)가 서로 같기 때문에 밑변의 비가 곧 넓이의 비입니다.

\(\quad\)\(\mathrm S_1:\mathrm S_2=\mathrm{BN}:\mathrm{CN}\)

\(\quad\)\(\displaystyle \frac{1}{2}\mathrm{AB\cdot AN}\sin\alpha:\frac{1}{2}\mathrm{AC\cdot AN}\sin\beta=\mathrm{BN}:\mathrm{CN}\)

\(\quad\)\(\mathrm{AB}\sin\alpha:\mathrm{AC}\sin\beta=\mathrm{BN}:\mathrm{CN}\)

내각의 이등분선

여기서 내분하는 각도가 서로 같아지면 다음의 비를 만족합니다.

\(\quad\)\(\mathrm{AB}:\mathrm{AC}=\mathrm{BN}:\mathrm{CN}\)

외각의 등분선

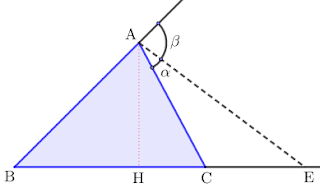
\(\triangle \mathrm{ABC}\)에서 꼭짓점\(\mathrm A\)의 외각을 \(\angle \alpha\)와 \(\angle \beta\)로 나누어진다고 할 때, \(\triangle \mathrm{ABE}\)의 넓이 \(\mathrm S_1\)과 \(\triangle \mathrm{ACE}\)의 넓이 \(\mathrm S_2\)는 다음과 같이 구해집니다.

\(\quad\)\(\displaystyle \mathrm S_1=\frac{1}{2}\mathrm{AB\cdot AE}\sin(\pi-\beta)\)

\(\quad\)\(\displaystyle \mathrm S_2=\frac{1}{2}\mathrm{AC\cdot AE}\sin\alpha\)

여기서 \(\sin(\pi-\beta)\)는 삼각함수의 덧셈정리에 의해서 다음과 같이 간단히 할 수 있습니다.

\(\quad\)\(\begin{align}\sin(\pi-\beta)
&=\sin\pi\cos\beta-\cos\pi\sin\beta \\
&=\sin\beta 
\end{align}\)

한편, \(\triangle \mathrm{ABE}\)과 \(\triangle \mathrm{ACE}\)의 꼭짓점 \(\mathrm A\)에서 변 \(\mathrm{BC}\)에 내린 수선의 발을 \(\mathrm H\)라 하면, 높이 \(\mathrm{AH}\)가 서로 같기 때문에 밑변의 비가 곧 넓이의 비입니다.

\(\quad\)\(\mathrm S_1:\mathrm S_2=\mathrm{BN}:\mathrm{CN}\)

\(\quad\)\(\displaystyle \frac{1}{2}\mathrm{AB\cdot AE}\sin\beta:\frac{1}{2}\mathrm{AC\cdot AE}\sin\alpha=\mathrm{BE}:\mathrm{CE}\)

\(\quad\)\(\mathrm{AB}\sin\beta:\mathrm{AC}\sin\alpha=\mathrm{BE}:\mathrm{CE}\)

외각의 이등분선

여기서 외분하는 각도가 서로 같아지면 다음의 비를 만족합니다.

\(\quad\)\(\mathrm{AB}:\mathrm{AC}=\mathrm{BE}:\mathrm{CE}\)

응용예제

응용예제1

두 점 \(\rm{A,B}\)를 지나는 직선이 점 \(\rm C(2,4)\)를 지날 때, \(\overline{\rm{AC}}=4\sqrt{5}\)이고, 점 \(\rm B\)는 선분 \(\rm{CA}\)를 \(1:3\)으로 외분한다. 점 \(\rm D(3,2)\)와 두 점 \(\rm {A,B}\)를 이은 삼각형 \(\rm{ABD}\)의 넓이가 최대일 때, \(\angle\rm{B}\)의 이등분선의 \(x\)절편은? (단, 점 \(\rm A\)의 \(x\)좌표는 점 \(\rm B\)의 \(x\)좌표보다 크다).

\(\quad\)\((1)\;\;-6-2\sqrt{5}\)

\(\quad\)\((2)\;\;-6+2\sqrt{5}\)

\(\quad\)\((3)\;\;-6-\sqrt{5}\)

\(\quad\)\((4)\;\;6-2\sqrt{5}\)

\(\quad\)\((5)\;\;6+2\sqrt{5}\)