원의 접선의 방정식

원문 보기: https://dawoum.duckdns.org/wiki/원의_접선의_방정식

Main article: Tangent lines to circles

원과 직선의 위치 관계에서 소개한 원과 직선의 교점이 1개인 경우에 대해, 그 직선은 접하는 직선, 또는 간단히 접선으로 불립니다. 이때, 주어진 상황에 따라 접선을 구하는 방법이 조금 다를 수 있습니다.

접선을 구하는 과정은, 원과 직선의 위치 관계에서 소개한 것처럼, 두 도형의 방정식에 대한 연립방정식을 푸는 것으로써, 결과로 제공되는 이차방정식이 중근을 갖는, 즉 그의 판별식 \(D=0\)이라는 조건을 이용합니다.

또 다른 방법은 기하학적으로 접근하는데, \(d=r\)의 조건으로부터 계산될 수 있습니다. 비록 항상 그런 것은 아닐지라도, 계산의 편의를 위해, 대체로 기하학적 방법을 이용합니다.

기울기가 주어진 경우

중심이 원점

기울기가 \(m\)이고 원 \(x^2+y^2=r^2\)에 접하는 접선의 방정식을 구합니다.

먼저 직선의 방정식을 \(y=mx+n\)으로 놓고 원의 방정식에 대입합니다. 여기서 교점이 1개이므로 판별식 D=0을 만족하는 \(n\)을 구할 수 있습니다.

\(\quad\)\(x^2+(mx+n)^2=r^2\)

\(\quad\)\((m^2+1)x^2+2mnx+n^2-r^2=0\)

\(\quad\)\(\displaystyle \frac{D}{4}=(mn)^2-(m^2+1)(n^2-r^2)=0\)

\(\quad\)\(n^2=r^2(m^2+1)\)

\(\quad\)\(\therefore n=\pm r\sqrt{m^2+1}\)

따라서 구하는 접선의 방정식은 다음과 같습니다.

\(\quad\)\(\therefore y=mx\pm r\sqrt{m^2+1}\)

중심이 임의의 점

이를 확장해서 중심의 좌표가 \(C(a,b)\)인 접선의 방정식을 구합니다. 위와 동일한 방법을 사용하면, 다음 두 식을 연립해서 판별식을 적용해야 합니다.

\(\quad\)\(\left\{\begin{align}
&(x-a)^2 + (y-b)^2 = r^2  \\
& y = mx+n 
\end{align}\right.\)

\(\quad\)\((x-a)^2+(mx+n-b)^2=r^2\)

\(\quad\)\((m^2+1)x^2-2(a-mn+bm)x+a^2+n^2+b^2-2nb-r^2=0\)

\(\quad\)\(\frac{D}{4}=(a-mn+bm)^2-(m^2+1)(a^2+n^2+b^2-2nb-r^2)=0\)

\(\quad\)\((n-b+am)^2=r^2(m^2+1)\)

\(\quad\)\(\therefore n = b-am\pm r\sqrt{m^2+1}\)

따라서 구하는 접선의 방정식은 다음과 같습니다.

\(\quad\)\(\therefore y=mx+b-am \pm r\sqrt{m^2+1}\)

이 방법은 계산하는데 시간이 걸리기 때문에 평행이동으로 해결할 수 있습니다.

중심이 원점에 있는 원에 접하는 기울기가 \(m\)인 접선을 잡고, 중심을 \(\mathrm C(a,b)\)이동시키면 원하는 접선을 얻을 수 있습니다.

\(\quad\)\(y=mx\pm r\sqrt{m^2+1}\)

\(\quad\)\(y-b=m(x-a) \pm r\sqrt{m^2+1}\)

\(\quad\)\(\therefore y=mx+b-am \pm r\sqrt{m^2+1}\)
위와 동일한 결과를 얻을 수 있습니다.

기하학적인 접근

원 \(x^2+y^2=r^2\)에 접하는 기울기 \(m\)이 주어진 접선의 방정식을 \(y=mx+n\)을 구해보겠습니다. 여기서는 원의 중심에서 직선까지 거리와 반지름이 같음을 이용합니다.

\(\quad\)\(mx-y+n=0\; (0,0)\)

\(\quad\)\(d=\frac{|n|}{\sqrt{m^2+1}}=r\)

\(\quad\)\(|n|=r\sqrt{m^2+1}\)

\(\quad\)\(n=\pm r\sqrt{m^2+1}\)

예제

원 \(x^2+y^2=4\)에 접하고 기울기가 3인 접선의 방정식을 구하여라.

해설) 접선을 \(y=3x+n\)로 두고, 중심인 원점에서 접선까지 거리가 반지름 2와 같음을 이용합니다.

\(\quad\)\(3x-y+n=0\; (0,0)\)

\(\quad\)\(d=\frac{|n|}{\sqrt{9+1}}=2\)

\(\quad\)\(|n|=2\sqrt{10}\)

\(\quad\)\(n=\pm 2\sqrt{10}\)

\(\quad\)\(\therefore y=3x\pm 2\sqrt{10}\)

접점이 주어진 경우

중심이 원점

원 \(x^2+y^2=r^2\) 위의 점 \(\mathrm P(x_1, y_1)\)을 지나는 접선의 방정식을 구합니다.

먼저 접점이 축 위에 있을 때에는 축과 나란한 식이므로 다음과 같이 쉽게 구해집니다.

\(\quad\)\(x-axis:\;x=x_1\)

\(\quad\)\(y-axis:\;y=y_1\) 

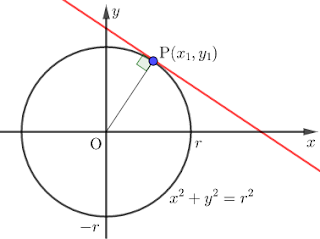접점이 축 위에 있지 않을 때에는, 오른쪽 그림에서처럼 접선의 기울기는 \(\mathrm{OP}\)의 기울기의 수직입니다. 그러므로, \(\mathrm{OP}\)의 기울기가 \(\frac{y_1}{x_1}\)이므로 접선의 기울기는 \(-\frac{x_1}{y_1}\)입니다. 

따라서 접선의 방정식은 지나는 한 점과 기울기를 알고 있으므로 다음과 같이 구해집니다.

\(\quad\)\(\therefore y-y_1=-\frac{x_1}{y_1}(x-x_1)\)

이 식의 양변에 \(y_1\)을 곱하고 다음과 같이 정리를 합니다.

\(\quad\)\(x_1x+y_1y=x_1^2+y_1^2\quad\cdots (1)\)

또한 접점은 원 위의 점이므로 원의 방정식에 대입했을 때, 식을 만족합니다.

\(\quad\)\(x_1^2+y_1^2=r^2\quad\cdots(2)\)

(2)식의 결과를 (1)식에 대입해서 접선의 방정식을 완성합니다.

\(\quad\)\(x_1x+y_1y=r^2\quad\cdots(3)\)

중심이 임의의 점

중심이 임의의 점일 때에도 위와 같은 방법으로 접선의 방정식을 구할 수도 있습니다. 여기서는 평행이동을 이용해서 접선의 방정식을 유도해 보겠습니다. 이미 구해진 공식을 이용하기 위해서 원점으로 평행이동을 한 후에, 원점에서의 접선을 구하고, 원래의 위치로 평행이동을 해서 접선의 방정식을 구할 것입니다.

먼저, 중심 \(\mathrm C(a,b)\)를 원점으로 이동해야 합니다. 그러므로 좌표의 평행이동에 따라 접점 \((x_1, y_1)\)이 \((x_1-a, y_1-b)\)로 이동됩니다.

이제 (3)식에 대입해서 원점이 중심인 원에서의 접선의 방정식을 구합니다.

\(\quad\)\((x_1-a)x+(y_1-b)y=r^2\)

이 접선을 x축으로 \(a\)만큼, y축으로 \(b\)만큼 이동시킵니다. 따라서 접선의 방정식은 다음과 같이 구해집니다.

\(\quad\)\((x_1-a)(x-a)+(y_1-b)(y-b)=r^2\quad \cdots(4)\)

원 밖의 한 점이 주어진 경우

원 내부의 점에서는 접선을 그릴 수 없고, 원주 위의 접점에서는 접선을 1개, 원 밖의 한 점에서는 2개의 접선을 항상 그릴 수 있습니다.

원 밖의 점 \(\mathrm P(p,q)\)에서 원 \((x-a)^2+(y-b)^2=r^2\)에 접선을 그었을 때, 그 방정식은 몇 가지 방법으로 구할 수 있습니다.

판별식을 이용

두 도형의 교점을 지나는 방정식으로 해결책을 찾을 수 있습니다. 점 \(\mathrm P(p,q)\)를 지나는 직선의 방정식을 다음과 같이 놓습니다.

\(\quad\)\(y-q=m(x-p)\quad \cdots(1)\)

이 접선의 방정식과 원의 방정식을 연립으로 풀어서 \(x,y\)에 관한 이차방정식을 만듭니다.

접선은 교점이 1개만 발생하는 경우이므로, 판별식 \(D=0\)을 이용하면 \(m\)에 관한 이차방정식을 만들 수 있습니다.

여기서 \(m\)이 서로 다른 두 개의 실근을 가지면 (1)식에 대입하면 두 개의 접선의 방정식을 구할 수 있습니다.

그러나 \(m\)이 중근을 갖는 경우에는 (1)식에 대입해서 1개의 접선의 방정식을 구할 수 있습니다. 나머지 1개의 접선은 기하학적으로 \(y\)축에 수직이면서 원에 접하는 식입니다. 즉, \(x=p\)가 나머지 1개의 접선의 방정식입니다.

이 방법은 모든 이차 곡선에 이용할 수 있지만, 다른 방법에 비해 계산이 복잡합니다.

접점을 이용

위에서 소개된 접점이 주어진 경우를 이용합니다. 접점을 \((x_1,y_1)\)으로 두면, 접선의 방정식을 다음과 같이 둡니다.

\(\quad\)\((x_1-a)(x-a)+(y_1-b)(y-b)=r^2\quad\cdots(1)\)

이제 접점을 구하면 접선의 방정식을 구할 수 있습니다.

먼저, 접선은 \(\mathrm P(p,q)\)를 지나가므로 다음을 만족합니다.

\(\quad\)\((x_1-a)(p-a)+(y_1-b)(q-b)=r^2\quad\cdots(2)\)

또한, 접점은 원 위의 점이므로 원의 방정식을 만족합니다.

\(\quad\)\((x_1-a)^2+(y_1-b)^2=r^2\quad \cdots(3)\)

이제 (2),(3)연립방정식을 풀어서 접점 \((x_1, y_1)\)을 구할 수 있습니다.

이 값을 (1)에 대입해서 직선의 방정식을 구합니다.

이 방법은 접점이 주어진 경우에 접선의 방정식을 구하는 방법이 알려져 있을 때만 사용할 수 있습니다. 장점으로는 판별식을 이용하는 것보다 계산이 조금 쉽습니다.

기하학적인 접근

원과 직선이 접하는 경우에는 중심에서 접선까지 거리가 반지름과 같음을 이용합니다.

점 \(\mathrm P(p,q)\)를 지나는 직선의 방정식을 다음과 같이 놓습니다.

\(\quad\)\(y-q=m(x-p)\quad \cdots(1)\)

중심에서 접선까지 거리와 반지름의 길이가 같음을 이용합니다.

\(\quad\)\(mx-y+q-mp=0,\;\;(a,b)\)

\(\quad\)\(\displaystyle d=\frac{|ma-b+q-mp|}{\sqrt{m^2+1}}=r\)

\(\quad\)\(|ma-b+q-mp|=r\sqrt{m^2+1}\quad\cdots(2)\)

(2)식의 양변을 제곱해서 m에 관한 방정식을 풉니다.

만약 \(m\)이 일차방정식이거나 \(m\)이 이차방정식이더라도 중근을 갖는 경우에는 (1)식에 대입해서 1개의 접선의 방정식을 구할 수 있습니다. 나머지 1개의 접선은 기하학적으로 \(y\)축에 수직이면서 원에 접하는 식입니다. 즉, \(x=p\)가 나머지 1개의 접선의 방정식입니다.

반면에 \(m\)에 관한 이차방정식이 만들어지고 서로 다른 두 개의 실근을 가지면 (1)식에 대입하면 두 개의 접선의 방정식을 구할 수 있습니다.

응용예제

응용예제1

좌표평면 위에 두 원 \(\mathrm{A, B}\)가 있습니다. 원 \(\mathrm{A}\)는 반지름의 길이가 1이고 중심이 직선 \(y=-x\) 위를 움직이고, 원 \(\mathrm{B}\)는 반지름의 길이가 2이고 중심은 직선 \(y=2x\) 위를 움직입니다. 이때, 두 원이 움직이는 영역의 공통부분의 넓이를 구하시오.

응용예제2

오른쪽 그림과 같이 두 원 \((x+2)^2+(y-3)^2=4\), \((x-2)^2+(y-1)^2=1\) 밖의 한 점 \(\mathrm P\)에서 두 원에 그은 접선의 길이가 항상 같을 때, 점 \(\mathrm P\)가 그리는 도형의 방정식은?

응용예제3

점 \(\mathrm{A}(3,4)\)에서 원 \((x+1)^2+(y-2)^2=16\)에 그은 두 접선이 \(x\)-축과 만나는 점을 각각 \(\mathrm{B,C}\)라고 할 때, 삼각형 \(\mathrm{ABC}\)의 넓이는?

응용예제4

\(x\)-축 위의 점 \((k,0)\)에서 원 \(x^2+y^2=1\)에 접선을 그을 때, 제1 사분면에 있는 접점을 \((x_k, y_k)\)이라고 놓습니다. 이때, \(y_2 \times y_3 \times \cdots \times y_{15}\)의 값을 구하는 과정을 서술하시오.

응용예제5

중심이 원점 \(\mathrm{O}\)이고 반지름의 길이가 1인 원 위에 5개의 임의의 점 \(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{C}\), \(\mathrm{D}\), \(\mathrm{E}\)에 대하여 삼각형 \(\mathrm{ABC}\)의 무게중심이 \(\mathrm{O}\)이고, 삼각형 \(\mathrm{ODE}\)는 정삼각형입니다. 선분 \(\mathrm{AB}\), \(\mathrm{AC}\),\(\mathrm{OD}\), \(\mathrm{OE}\)의 연장선 위에 점 \(\mathrm{B'}\), \(\mathrm{C'}\), \(\mathrm{D'}\), \(\mathrm{E'}\)가 놓여 있습니다. 두 반직선 \(\mathrm{BB'}\), \(\mathrm{CC'}\)과 선분 \(\mathrm{BC}\)에 동시에 접하는 원의 중심을 \(\mathrm{P}\)라 하고, 두 반직선 \(\mathrm{DD'}\), \(\mathrm{EE'}\)과 선분 \(\mathrm{DE}\)에 동시에 접하는 원의 중심을 \(\mathrm{Q}\)라 할 때, 선분 \(\mathrm{PQ}\)의 길이의 최댓값과 최솟값의 곱은?

응용예제6

점 \(\mathrm{P}(a,b)\)가 원 \((x-1)^2+(y-2)^2=10\) 위의 점일 때, \(3a-b\)의 최댓값은?

응용예제7

양수 \(k\)에 대하여 직선 \(y=3x+k\) 위의 점 \(\mathrm{P}\)에서 원 \(x^2+y^2=2\)에 그은 두 접선이 서로 수직이 되게 하는 점 점 \(\mathrm{P}\)가 오직 하나만 존재할 때, \(k\)의 값을 구하면?

응용예제8

자연수 \(n\)에 대하여 원 \((x-2n)^2+y^2=1\)과 원점을 지나는 직선이 제1 사분면에서 접할 때, 이 직선의 기울기를 \(a_n\)이라 하자. \(a_1^2+a_2^2+\cdots+a_{24}^2\)의 값은?

응용예제9

두 원

\(\quad\)\(C_1:\; x^2+y^2=25\),

\(\quad\)\(C_2:\; (x-2)^2-a^2=1\)

에 대하여 그림과 같이 원 \(C_2\)가 원 \(C_1\)에 내접하고 있다. 원점을 \(\mathrm{O}\), 내접하는 점을 \(\mathrm{A}\), 공통접선이 \(x\)축과 만나는 점을 \(\mathrm{B}\)라 할 때, 삼각형 \(\mathrm{OAB}\)의 넓이를 구하시오. (단, \(a\)는 양의 실수이다.)

응용예제10

직선 \(l\)은 반지름의 길이가 1인 원의 중심에서 2만큼 떨어져 있다. 직선 \(l\) 위의 임의의 한 점 \(\mathrm{P}\)에서 이 원에 두 접선을 그을 때, 두 접점 \(\mathrm{A,B}\)를 지나는 직선은 점 \(\mathrm{P}\)의 위치에 관계없이 한 점 \(\mathrm{Q}\)를 지난다. 이때, 원의 중심과 점 \(\mathrm{Q}\) 사이의 거리를 구하시오.

응용예제11

좌표평면에서 중심이 \((1,1)\)이고 반지름의 길이가 1인 원과 직선 \(y=mx\;(m>0)\)가 두 점 \(\mathrm{A,B}\)에서 만난다. 두 점 \(\mathrm{A,B}\)에서 각각 이 원에 접하는 두 직선이 서로 수직이 되도록 하는 모든 실수 \(m\)의 값의 합은?