구분구적법

원문 보기: https://dawoum.duckdns.org/wiki/구분구적법

See also: Quadrature (mathematics), Method of exhaustion, The Quadrature of the Parabola, and Riemann integral

직선으로 이루어진 다각형의 넓이를 구하는 문제는 삼각형과 사각형의 넓이를 구하는 방법이 알려졌었기 때문에, 다각형을 여러 개의 삼각형 또는 사각형 또는 둘을 섞어서 그의 넓이를 구했습니다. 이 값은 구하고자 하는 원래 도형의 넓이와 항상 일치합니다.

반면에, 일부가 곡면으로 이루어진 도형의 넓이를 구하는 문제는 이미 알려진 삼각형 또는 사각형 등의 넓이를 구하는 공식을 활용하고, 오차를 줄이기 위해, 마찬가지로 여러 개의 삼각형 또는 사각형으로 나누어서 접근하는 방법이 고대 그리스로부터 있었습니다. 그러나, 이 방법은 원래 도형에 대한 정확한 넓이를 구할 수 없었고 항상 오차를 포함하고 있었습니다.

이 방법에 극한의 개념을 적용해서, 즉, 무한한 개수로 나누면, 거의 오차를 영으로 만들 수 있다는 개념이 구분구적법입니다. 이것의 첫 번째 엄격한 정의는 베른하르트 리만이 만들었었고, 리만 적분이라고 부르기도 합니다.

원주의 길이와 원의 넓이

우리는 이전 과정에서 반지름의 길이, \(r\)을 알고 있으면, 원의 둘레의 길이는 \(2\pi r\)임을 배웠고, 원의 넓이는 \(\pi r^2\)임을 배웠습니다.

이제, 구분구적법을 통해서 원주의 길이를 공식화 해보려 합니다.

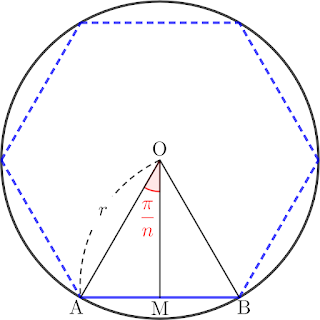
그림처럼, 같은 원에 정다각형의 변의 개수가 늘어날수록 원의 넓이와 오차가 줄어듬을 볼 수 있습니다.

한편, 무한대 개수의 변의 길이를 적용하기 위해, 그림에는 정육각형이 내접하고 있지만, \(n\) 개의 변을 갖는 정다각형으로 생각하십시오.

물론, 원주의 길이는 \(n\)개의 호 \(\overset\frown{\mathrm{AB}}\)로 이루어집니다.

여기서, 선분 \(\overline{\mathrm{AB}}\)의 길이와 호 \(\overset\frown{\mathrm{AB}}\)의 길이는 같지 않지만, \(n \to \infty\)를 보냄으로써, 오차를 0으로 만들 수 있습니다.

또한, 원주각 \(\angle{\mathrm{AOB}}\)는 원의 중심각, \(2\pi\)를 \(n\) 개로 나눔으로써,

\(\quad\)\(\displaystyle \angle{\mathrm{AOB}}=\frac{2\pi}{n}\)

그 각의 절반에 해당하는 \(\angle{\mathrm{AOM}}\)은

\(\quad\)\(\displaystyle \angle{\mathrm{AOM}}=\frac{\pi}{n}\)

게다가, 직각삼각형 \(\triangle{\mathrm{AOM}}\)에서,

\(\quad\)\(\displaystyle \overline{\mathrm{AM}}=r\sin{\frac{\pi}{n}}\)

따라서, 원주의 길이는 다음과 같은 극한으로 구할 수 있습니다.

\(\quad\)\(\begin{align}
\lim_{n \to \infty} l_n & =\lim_{n \to \infty} n \cdot \overline{\mathrm{AB}} \\
& = \lim_{n \to \infty} n \cdot 2\overline{\mathrm{AM}} \\
& = \lim_{n \to \infty} n \cdot 2r\sin{\frac{\pi}{n}} 
\end{align}\)

여기서 \(\displaystyle x=\frac{1}{n}\)으로 두면, \(n \to \infty\)일 때, \(x \to 0\)이므로,

위의 식에 이어서 원주의 길이는

\(\quad\)\(\displaystyle \begin{align}
\lim_{n \to \infty}l_n & = \lim_{x \to 0} 2r \cdot\frac{\sin \pi x}{x} \\
& = 2\pi r
\end{align}\)

마지막에 결과가 \(\displaystyle \lim_{x \to 0} \frac{\sin \pi x}{x}=\pi\)가 나오는 삼각함수의 극한은 미적분학2에서 배웁니다.

다음으로 원의 넓이는

\(\quad\)\(\displaystyle \begin{align}
\lim_{n \to \infty}S_n & =\lim_{n \to \infty} n \cdot \triangle\mathrm{AOB} \\
& = \lim_{n \to \infty} n \cdot 2\cdot\triangle\mathrm{AOM} \\
& = \lim_{n \to \infty} n \cdot 2\cdot\frac{1}{2}\left(r\sin{\frac{\pi}{n}}\right)\cdot \left(r\cos{\frac{\pi}{n}}\right) \\
\end{align}\)

여기서 \(\displaystyle x=\frac{1}{n}\)으로 두면, \(n \to \infty\)일 때, \(x \to 0\)이므로,

\(\quad\)\(\displaystyle \begin{align}
\lim_{n \to \infty}S_n & = \lim_{x \to 0} r^2 \cdot \left(\frac{\sin{\pi x}}{x}\right)\cdot \cos \pi x \\
& = \pi r^2 \\
\end{align}\)

마지막에 결과가 \(\displaystyle \lim_{x \to 0} \cos \pi x=1\)가 나오는 삼각함수의 극한은 미적분학2에서 배웁니다.

한편, 원에 구분구적법을 적용할 때, 원에 외접하는 다각형으로 접근할 수도 있습니다.

위의 원에 내접하는 다각형으로 접근할 때에는 구하려는 값보다 작은 쪽에서 오차가 0으로 접근하는 방식이고, 반면에 원에 외접하는 다각형으로 접근할 떼에는 구하려는 값보다 큰 쪽에서 오차가 0으로 접근하는 방식입니다.

함수와 \(x\)-축 사이의 넓이

Main article: Riemann integral

함수 \(y=x^2\)과 \(x\)-축 및 \(x=1\)로 둘러싸인 넓이 \(S\)를 구분구적법으로 구할 수 있습니다. 

원에서는 내접하는 정다각형의 변의 개수를 무한히 많게 함으로써 오차를 0으로 만들었습니다. 이때, 원주 또는 넓이를 쉽게 계산하기 위해, 중심으로부터 \(n\)개의 같은 (이등변) 삼각형을 그려서 접근했습니다.

함수에서는 구간에서 \(x\)-축으로 둘러싸인 부분을 같은 모양의 도형으로 나누는 것이 대체로 불가능합니다. 그래서, 함수의 특징, 즉, 정의역의 원소, \(x\)를 선택하면, 치역, \(y\)를 출력하므로, 정의역의 구간을 \(n\)개로 나누고, 이것을 직사각형의 밑변으로 삼습니다.

한편, 나누어진 구간의 \(x\)-좌표를 대입한 함숫값을 높이로 삼는데, 구간을 \(n\)로 나누면, \(x\)-좌표는 \(n+1\)개가 생기고, 오른쪽 \(n\) 개를 높이로 삼는 방법과, 왼쪽 \(n\) 개를 높이로 삼는 방법을 고등학교 교과서에서 소개하고 있습니다. 

첫 번째, 오른쪽의 함숫값을 높이를 사용하는 방법을 적용해 보면 (위의 그림), \(n\)개의 \(x\)-좌표는 다음과 같습니다.

\(\quad\)\(\displaystyle \frac{1}{n},\;\frac{2}{n},\;\frac{3}{n},\;\cdots,\;\frac{n}{n}\)

그리고, 이에 해당하는 함숫값, 즉 직사각형의 높이는 다음과 같습니다.

\(\quad\)\(\displaystyle \left(\frac{1}{n}\right)^2,\;\left(\frac{2}{n}\right)^2,\;\left(\frac{3}{n}\right)^2,\;\cdots,\;\left(\frac{n}{n}\right)^2\)

따라서, \(n\)개의 직사각형의 넓이는

\(\quad\)\(\begin{align}
S_r & =\frac{1}{n}\left(\frac{1}{n}\right)^2+\frac{1}{n}\left(\frac{2}{n}\right)^2+\frac{1}{n}\left(\frac{3}{n}\right)^2+\cdots+\frac{1}{n}\left(\frac{n}{n}\right)^2 \\
& = \frac{1}{n^3}\left(1^2+2^2+3^2+\cdots+n^2\right) \\
& = \frac{1}{n^3}\cdot \frac{n(n+1)(2n+1)}{6}
\end{align}\)

오른쪽 함숫값을 사용했을 때, 이 함수에서는 원래의 넓이보다 큰데, 왜냐하면, 증가함수이기 때문입니다. 만약 감소함수이면, 오른쪽 함숫값을 사용한 것이 오히려 구하려는 넓이보다 작습니다. 그리고 구간에서 증감이 변하면, 비록 구할 수 있다고 할지라도, 어떤 넓이가 큰지 직관적으로 짐작하기 어렵습니다.

두 번째, 왼쪽의 함숫값을 높이를 사용하는 방법을 적용해 보면, \(n\)개의 \(x\)-좌표는 다음과 같습니다.

\(\quad\)\(\displaystyle 0, \frac{1}{n},\;\frac{2}{n},\;\frac{3}{n},\;\cdots,\;\frac{n-1}{n}\)

그리고, 이에 해당하는 함숫값, 즉 직사각형의 높이는 다음과 같습니다.

\(\quad\)\(\displaystyle 0^2,\;\left(\frac{1}{n}\right)^2,\;\left(\frac{2}{n}\right)^2,\;\left(\frac{3}{n}\right)^2,\;\cdots,\;\left(\frac{n-1}{n}\right)^2\)

따라서, \(n\)개의 직사각형의 넓이는

\(\quad\)\(\begin{align}
S_l & =0\cdot 0^2+\frac{1}{n}\left(\frac{1}{n}\right)^2+\frac{1}{n}\left(\frac{2}{n}\right)^2+\frac{1}{n}\left(\frac{3}{n}\right)^2+\cdots+\frac{1}{n}\left(\frac{n-1}{n}\right)^2 \\
& = \frac{1}{n^3}\left(1^2+2^2+3^2+\cdots+(n-1)^2\right) \\
& = \frac{1}{n^3}\cdot \frac{(n-1)n(2n-1)}{6}
\end{align}\)

왼쪽 함숫값을 사용했을 때, 이 함수에서는 원래의 넓이보다 작은데, 왜냐하면, 증가함수이기 때문입니다. 만약 감소함수이면, 왼쪽 함숫값을 사용한 것이 오히려 구하려는 넓이보다 큽니다.

어쨌든, 나누는 개수를 무한히 많게, 즉, \(n \to \infty\)하면,

\(\quad\)\(\displaystyle \lim_{n \to \infty} S_r = \lim_{n \to \infty} S_l =\frac{1}{3}\)

따라서, 구하려는 넓이, \(S\)는

\(\quad\)\(S_l < S <S_r\)

이고, 샌드위치 정리에 의해 \(S=\frac{1}{3}\)입니다.

구분구적법에서 생각해야 할 점

밑변

주어진 \(x\)-좌표와 상관없이 오른쪽 좌표에서 왼쪽 좌표를 빼기 때문에, 밑변은 항상 양수입니다.

위의 구분구적법은 구간의 길이가 1이고, 그것을 \(n\) 개로 나눔으로써, 밑변의 길이는 \(\frac{1}{n}\)입니다. 만약 구간의 길이가 \(p\)이면, 그것을 \(n\) 개로 나눔으로써, 밑변의 길이는 \(\frac{p}{n}\)입니다.

\(n+1\) 개의 좌표

먼저, 구간 [0,2]와 같이 길이가 2로 바뀌면, 이것을 \(n\) 개의 구간으로 나누면, 각 좌표는

\(\quad\)\(\displaystyle 0,\;\frac{2}{n},\;\frac{4}{n},\;\frac{6}{n},\;\cdots,\;\frac{2n}{n}\)

게다가, 구간 [1,3]와 같이 시작점이 0이 아니면,

\(\quad\)\(\displaystyle 1,\;1+\frac{2}{n},\;1+\frac{4}{n},\;1+\frac{6}{n},\;\cdots,\;1+\frac{2n}{n}\)

높이, 넓이, 그리고 구분구적법

원주와 원의 넓이는 길이들이 전부 양수입니다. 따라서, 곱의 부호는 항상 양수이므로 부호를 고려할 필요가 없었습니다.

그러나, 함수의 구분구적법에서는 높이는 함숫값에 해당하므로, 그래프가 \(x\)-축 위에 그려질 때, 높이(함숫값)가 양수이지만, 그래프가 \(x\)-축 아래에 그려질 때, 높이는 음수입니다.

따라서, 그래프가 \(x\)-축 위에 그려질 때, 구분구적법의 결과는 양수이므로, 그 자체가 넓이입니다. 반면에, 그래프가 \(x\)-축 아래에 그려질 때, 구분구적법의 결과는 음수이므로, 넓이는 절댓값을 취해서 얻어야 합니다.

게다가, 그래프의 중간에서 \(x\)-축을 가로지를 때에는, 그래프가 \(x\)-축 위에 그려진 부분과 그래프가 \(x\)-축 아래에 그려진 부분을 따로 계산해야 합니다. 그러기 위해서, 함수의 근이 구간 안에 존재하는지 확인이 필요하며, 근을 구하는 과정이 먼저 이루어져야 함을 의미합니다.