함수의 극대와 극소

원문 보기: https://dawoum.duckdns.org/wiki/함수의_극대와_극소

이차함수는 실수 전체의 구간에 대해 꼭짓점에서 최댓값 또는 최솟값을 가집니다.

한편, 다른 함수, 예를 들어, 삼차함수는 전 구간에 걸쳐 최댓값 또는 최솟값이 존재하지는 않습니다. 그러나, 구간을 적절히 잘 정하면, 그 구간 내부에서 최댓값 또는 최솟값을 가질 수 있습니다.

이때, 그 구간 전체에 걸쳐 증가 또는 감소가 아닌 경우, 즉, 증가상태에서 감소상태로 바뀌는 점 또는 반대로, 감소상태에서 증가상태로 바뀌는 점이 존재할 수 있습니다. 그 점이 구간 내부에서 최댓값 또는 최솟값이 될 수도 있지만, 그렇지 않을 수도 있으므로, 극점이라는 새로운 용어로 불립니다.

함수의 극대·극소

함수 \(y=f(x)\)가 \(x=a\)에서 연속이고, \(x=a\)의 왼쪽과 오른쪽에서

• \(f(x)\)가 증가상태에서 감소상태로 바뀔 때, \(f(x)\)는 \(x=a\)에서 극대라 하고, \(f(a)\)를 극댓값이라고 합니다.
• \(f(x)\)가 감소상태에서 증가상태로 바뀔 때, \(f(x)\)는 \(x=a\)에서 극소라 하고, \(f(a)\)를 극솟값이라고 합니다.

여기서, 극대와 극소를 전부 극점이라고 합니다.

게다가, 극점은 미분가능할 필요는 없고, 반드시 그 점에서 연속이어야 합니다. 즉, 꺾어진 점은 미분가능하지 않지만, 연속이므로, 극점이 될 수는 있습니다.

도함수를 통한 극대·극소

비록 어떤 점이 미분 가능하지 않을지라도, 그 점에서 연속이고 증가상태에서 감소상태로 변하거나, 반대로 감소상태에서 증가상태로 변하는 극점입니다. 

한편, 함수의 증가와 감소#도함수를 통한 증가상태와 감소상태에서, 함수 \(y=f(x)\)가 주어진 구간에서 미분 가능하고, 도함수가 양수인 증가상태에서 도함수가 음수인 감소상태로 변하거나, 또는 반대로 감소상태에서 증가상태로 변할 때, 즉, \(x=a\)에서 극점이 되려면, \(f'(a)=0\)이어야 합니다.

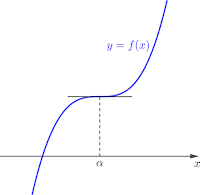
반면에, 비록 \(f'(a)=0\)이라고 할지라도, 극점이 되지 않는 경우가 있습니다. 예를 들어, \(y=x^3\)은 영에서 \(f'(0)=0\)이지만, 증감이 변하지 않기 때문에, 극점이 될 수 없습니다.

특히 다항함수에서, 그의 도함수의 근이 홑근과, 삼중근, 오중근 등의 홀수 중근일 때에는 증감이 변하기 때문에 극점이 될 수 있고, 반면에 이중근, 사중근 등의 짝수 중근은 증감이 변하지 않기 때문에 극점이 될 수 없습니다.

극대와 극소의 판정

일반적으로 미분가능한 함수 \(y=f(x)\)가 \(x=a\)에서 극값을 가지려면,

1. \(f'(a)=0\)이고,
2. \(x=a\)의 왼쪽과 오른쪽에서 증감상태가 바뀌므로, 즉 도함수 \(f'(x)\)의 부호가 바뀝니다.

보통, 이것을 표로 만들어서 극대인지 극소인지 판정을 합니다. 그리고 이것을 증감표라고 부릅니다.

다항함수의 극대와 극소

미분가능한 함수는 극대와 극소의 판정은 증감표를 이용하거나, 나중에 이계도함수를 배운 후에, 이계도함수의 부호로 판정을 합니다. 어쨌든, 이 방법은 상당히 귀찮습니다.

한편, 이차함수의 최대 최소에서, 선행 계수가 양수이면 극솟값, 즉, 최솟값을 가지고, 반면에, 선행 계수가 음수이면, 극댓값, 즉, 최댓값을 가집니다. 이것은 그래프의 개형 통해서 이미 그의 형태를 알고 있기 때문에, 증감표의 작성 없이 판정이 가능합니다.

고등학교 교과과정에서, 다항함수는 삼차함수와 사차함수 정도가 고려되기 때문에, 삼차함수와 사차함수의 개형을 알고 있을 필요가 있습니다.

게다가, 이차함수에서는 도함수가 영이 되는 점이 반드시 홑근 1개 존재하므로 그 점은 반드시 극점이 되지만, 삼차함수와 사차함수는 도함수가 영이 되는 점의 개수는 그래프의 개형에 따라 다르고, 또한, 홀수 중근 또는 짝수 중근을 고려해서 극점을 판정해야 합니다.

먼저, 이차함수와 마찬가지로, 선행 계수가 양수인 것에 대해 그래프의 개형을 다루고, 선행 계수가 음수이면, \(x\)-축에 대칭이 형태로 그래프의 개형을 생각할 수 있으므로, 여기서는 선행 계수가 양수인 경우만 다룹니다.

삼차함수의 그래프의 개형

삼차함수 \(f(x)=ax^3+bx^2+cx+d\) (\(a > 0\))에서, 그의 도함수

\(\quad\)\(f'(x)=3ax^2+2bx+c\)

는 그의 근의 유형에 따라 3가지 형태의 개형을 가집니다. 게다가 도함수가 이차함수이기 때문에, 이차함수의 판별식을 이용할 수 있습니다.

첫 번째, 도함수를 영으로 만드는 근이 서로 다른 두 실근, 즉 \(D>0\)이면, 극대와 극소를 1개씩 가지고, 또한, 근의 위치가 \(\alpha<\beta\)라고 하면, 극댓값 \(f(\alpha)\), 극솟값 \(f(\beta)\)를 가집니다.

두 번째, (이)중근을 가지면, 세 번째, 허근을 가지면, 극값을 가지지 않습니다.

사차함수의 그래프의 개형

사차함수 \(f(x)=ax^4+bx^3+cx^2+dx+e\) (\(a > 0\))에서, 그의 도함수

\(\quad\)\(f'(x)=4ax^3+3bx^2+2cx+d\)

는 그의 근의 유형에 따라 4가지 형태의 개형을 그릴 수 있지만, 극점의 관점에서는 극점이 3개인 경우와 극점이 1개인 경우의 2가지로 해석할 수도 있습니다.

첫 번째, 도함수를 0으로 만드는 근이 서로 다른 세 실근을 가지고, 근의 위치가 \(\alpha < \beta < \gamma\)라고 하면, 극댓값 \(f(\beta)\), 극솟값 \(f(\alpha), f(\gamma)\)를 가집니다.

두 번째, 하나의 중근과 중근과 다른 실근 하나를 가질 때, 중근에서는 극값을 가지지 않고, 다른 실근에서 극솟값을 가집니다. 예를 들어, \(\alpha, \alpha, \beta\)의 근을 가지면, \(\beta\)에서 극솟값 \(f(\beta)\)을 가지고, 반면에, \(\alpha, \beta, \beta\)의 근을 가지면, \(\alpha\)에서 극솟값 \(f(\alpha)\)을 가집니다.

 

세 번째, 하나의 실근과 다른 2개의 허근을 가질 때, 실근에서 극솟값을 가지는데, 그래프는 직전의 모양에서 중근을 가진 부분이 더 늘어져서 좀 더 펴지는 모양입니다. 

네 번째, 삼중근을 가질 때, 삼중근에서 극솟값을 가지고, 이차함수의 모양과 유사합니다.

추가적으로 짝수함수이면, 삼중근을 갖거나, 하나의 실근과 두 허근을 가질 때, 이차함수와 유사한 모양이 될 수 있습니다. 그리고, 이것이 평행이동이 된 그래프를 생각할 수 있습니다.